height of the hthcv flagpole problem
problem statement & process and solution: |
The easiest way to explain similarity is "Same shape, different size", that's what Mr. Carter told us after we did an activity that we redraw a shape in a bigger size using an expo marker and a rubber band. Then we were given a paper that asked us what we were trying to do. "What is the height of the HTHCV flagpole?" The main learning points was finding x (the height) in different methods (shadow, mirror and clinometer.) Following that we wrote down our initial guess for the height. My minimum 25 ft, maximum 40 ft.
|
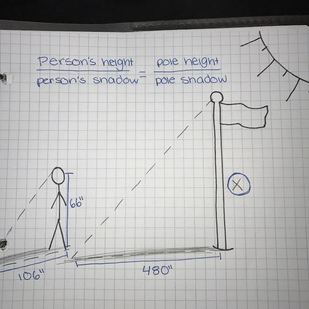
Shadow method:First we drew a representation of what we mean by using the shadow to find x. We know all the angles because of the 90 degrees of the floor to the pole/person, this created two triangles. Also the sun provides a fixed angle so we know that as well, aka the (AA) theorem. Then we set up a proportion "Person's height/person's shadow = pole height/pole shadow"
|
Then we used the proportion that we made and plugged in the measurements that we got as you can see in the picture. We then continued solving for x by cross multiplying and getting 298.867925 we divided that number by 12 to convert it into feet and then got 24.9 so we rounded up to 25 ft.
|
mirror method:
|
We were given this worksheet and the problem was to figure out the height and distance from the mirror for each spider. This introduced us the mirror method.
|
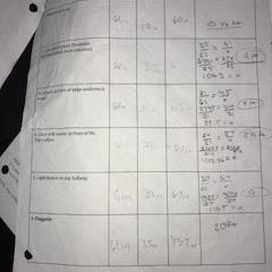
We applied what we learned there to the worksheet ¨mirror magic" and then we went around the school to apply this method to 6 different objects. The last one was the flag pole and we ended up with 20 ft. This was the lowest estimate of the whole class. We had doubt in it so me and another group mate went back to the flagpole and did the method again. A mirror was laid on the group and a person would look into the mirror to see the top of the object. Then we measured the height of the person and the distance of the person to the mirror, then the distance of the mirror to the flagpole. We were then able to set up a proportion because we can use the angle angle theorem. The two triangles that we can form both have a right angle, and a fixed angle because of the mirror.
Mirror to person- 35 in. Person´s height- 61 in. Mirror to flagpole- 137 in. 35/61 = 137/x 35x = 8,357 35x/35 = 8,357/35 x = 238.9 or 239 239/12 = 19.9 we rounded up to 20 ft. |
clinometer method: |
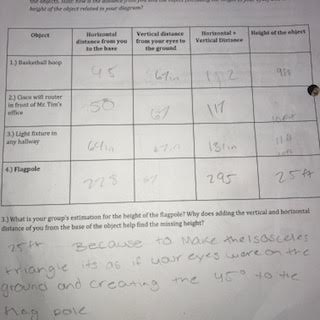
Isosceles triangles are when two sides are equal in a triangle. What we did was use the clinometer up to one of our eyes to look through the straw. Then someone else would move that person until the angle on the clinometer reads 45 degrees. Then we measured up to the persons eye, that stayed the same for each object we did. Also we measured the person to the object.
Person to flagpole- 228 in. Person´s eyes- 67 in. 228 + 67 = 295/12 = 24.5 ft. The reason we added the two measurements together because the triangle doesn´t end at our eyes because it won´t be 45 degrees. So we added them together to be as if our eyes were on the floor when we were using the clinometer. |
best final estimation: |
I think the height of the hthcv flagpole is around 25 ft. After doing these methods which is not 100% accurate, I can see that I was close to 25 ft. each time. Out of all the methods, I liked the shadow method the best and I felt like that one was the most accurate, plus I did get 25 ft on that one.
|
Problem evaluation: |
I did like this problem but it isn´t one of my favorites. At first I didn´t understand it and I struggled with setting up the proportions. Now it is really simple to do so. I still don´t feel confident with my final estimation but that is what I got, I wish we had another method to check. This problem did really challenge my thinking and made me grow so much in math. Now I am able to explain and teach others my thinking.
|
self EVALUATION: |
I think I would grade myself an A. I did do all the work and turned them in on time. I also asked my peers when I needed help and Mr. Carter as well. The one thing I think I could have done to bring it up to an A+ would be going to tutoring one day in the beginning when I didn´t understand how to set up the proportion. I caught on quickly and now on the star problem 3 I am able to do the altitude of the triangle!
|
Peer critique & what i changed:
|
My peer Thomas critiqued my page and gave me cool and warm feedback to make this write up so much better.
Warm: -Lots of photos -Clear labeling -Good explanations Cool: -Mention the theorem in in Shadow method -Make the titles bold -Organized What I fixed: I made all of the titles bold as well as included a similarity theorem in the shadow method. |
My other peer Aaron critiqued my page as well and gave me even more cool and warm feedback.
Warm: - Organized -Short and to the point -Understandable -Professional Cool: -Typo -Add more to problem evaluation What I fixed: I fixed the typo ad I also added more to the problem evaluation section. |