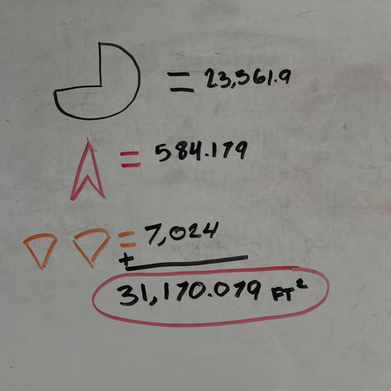Cow Problem
Problem Statement:
The cow problem started with a farmer who had his cow attached to a 10' x 10' barn at an outside corner by a 100' rope. The farmer is only going to plant grass to wear the cow can roam, so we needed to figure out how many square ft. of grass the farmer needed to plant.
The cow problem started with a farmer who had his cow attached to a 10' x 10' barn at an outside corner by a 100' rope. The farmer is only going to plant grass to wear the cow can roam, so we needed to figure out how many square ft. of grass the farmer needed to plant.
|
Process:
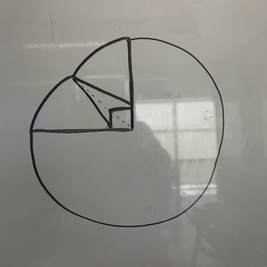
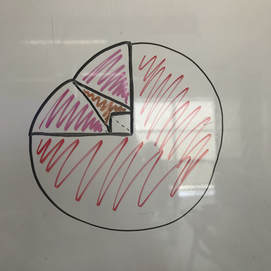
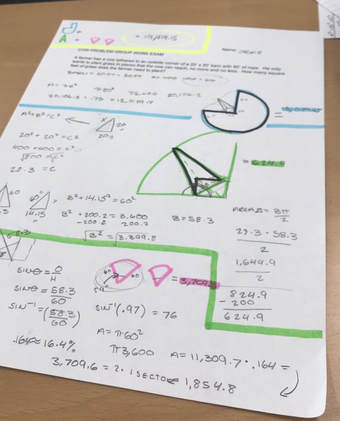
The first step we took to figure out this problem was to make our self a visual so we have a better understanding. We started off with the square 10' x 10' barn then attached the rope to an corner, I chose the bottom right. Then we put a point 100' out from the top, bottom, and two sides then connected them. This gave us 3/4 of a circle. The cow would get stuck at the first turn he makes to his left or right, and since his rope is only 100ft and the barn is 10ft, it would shorten it by 10ft. So next I continued from the 100ft we marked from the top and the left but with 90ft of rope. This created what we called a "dimple" in the circle. Our next obstacle as a class was to figure out how to divided this off shaped circle into shapes that we were able to calculate the area of. I attached a line from the dimple to the 2 corners of the barn as shown. Then because we have no idea how to calculate that arrow shape we created a triangle by splitting the barn in half. This also created sectors that we can find the area of. Our end product of the visual look very complicated at first. (2) We also had to use the following formulas throughout the problem. Area of a circle= πr² Area of a triangle= bh/2 Area of a square= LW Phythagorean Theorem= a²+b²=c² SIN= O/H |
|
Solution:
To find the solution we have already broken down the shape into 3 that we can calculate, the 3/4 of a circle, the triangle-arrow shape and the sectors. 3/4 of a circle...
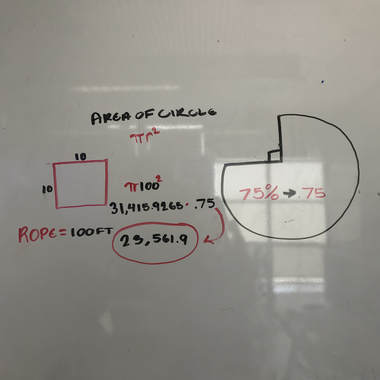
To find this is it was quite easy. We already have the formulas above so we just applied it. The radius of this circle is 100, why? Is this rope is attached onto a corner and can go 100 straight across to create a circle, the diameter would be 200, the radius therefore is 100. So we plug it in, π(100)² =31,415.9265. Now with this we will multiply by .75 because we are calculating 3/4th of a circle, 75% aka .75 of a circle. 31,415.9265 ⋅ .75 = 23,561.9 Triangle-Arrow shape...
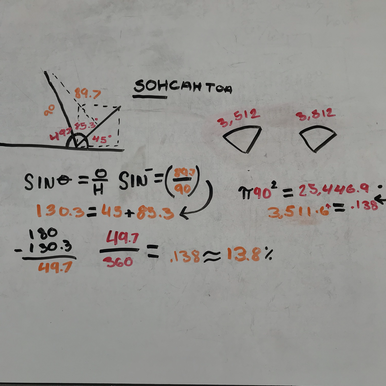
This one is a little bit more complicated. So first like I said before, we split up the barn to make a triangle, now we have a half of a barn with dimensions of 10',10',x. To find x will give us the base of the triangle we created. Plugging it into the Phythagorean Theorem gave us 10²+10²=C² . The reason why it is ordered like this is because C is always the hypotenuse which is the longest side, and A and B doesn't matter in this case. It turns into 100+100=C² , 200=C² Then we square root the 200 and C² and we are left with 14.14. Now we can use that as the base of our 90,90,14.14 triangle. The reason why we know its 90 is because when the rope of 100' got caught onto the corner of the barn it shortened to 90 and then we drew a line connected it to the dimple. We do not know the height of that triangle to solve for the area so I split the triangle in half and used the Phythagorean Theorem again, but this time we know C and need to find either A or B, doesn't matter which letter you use. A²+7.07²=90². Which turns into A²+50=8100, then A²=8050 then you find the square root and then A=89.7 aka the high of the triangle. Now we can plug that into the finding the area formula (BH/2) and get 14.14 times 89.7/2= 634.179 - 50 because we used half of the barn which is 100 in area and half is 50 so we subtract 50 from 634.179 and get 584.179, the area of the triangle-arrow shape. The sectors...
To calculate the area of the sectors, I drew the angles we needs to calculate. We already had one since we used half of the barn which was 90 degrees so we know we have 45 degrees. To calculate the area of the angle inside the triangle we have to use SOHCAHTOA. For the area we need to find we can use the Opposite of the angle measure and the Hypotenuse, so SIN. I plugged in our knowns and solved for the angle. SIN-=(89.7/90) gave us the angle measure 83.3. The other angle we need is easy. We know that the straight line's angle has to be 180, so we subtract our known angles from that. 180-83.3-45=49.7! Now to calculate the area of the sector, we have the angle measure and the lengths. We know that the angle measure is 90 because it got caught on a corner, so that makes a circle with the radius 90. The area of that circle is π(90)²=25,446.9 and because we need only that sector of the circle we will find how much area the angle covers. 49.7/360=.138 which is 13.8% of the circle. So we just multiply 25,446.9 times .138 and each one of our sectors is 3,512! To find the total area now we just have to add up all of our areas from the 3 different shaped and viola! The farmer should plant grass in a total of 31,170.079 ft²!
|
|
Evaluation/Reflection:
What really challenged me during this problem was SOHCAHTOA. When learning it freshman year I had no idea why we needed it and what it was used for. After learning it through the cow problem it defiantly benefited me and will be used during future math classes! I learned many new concepts besides SOHCAHTOA like using pi and the square root of a number and area of a sector and triangle. The group quiz we took defiantly benefited me and helped me understand the steps much clear with new dimensions and in a way shorter amount of time. We were very proud of the work we did on the group quiz we even took a picture of it after! I would grade myself an A+ not just because it's a good grade, but I did help my peers learn the concepts that I got right away and I wasn't afraid to ask them for help myself. Also I feel like I could teach this myself now to anyone who doesn't know any of the formulas we used.