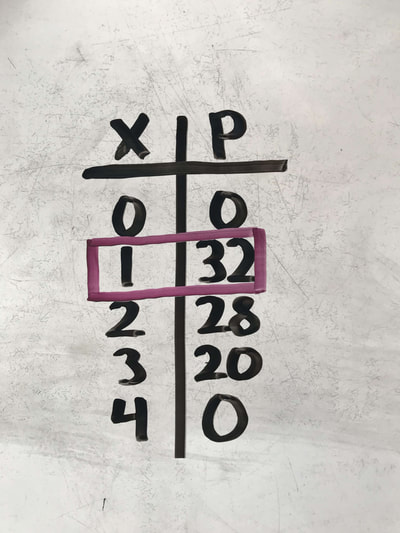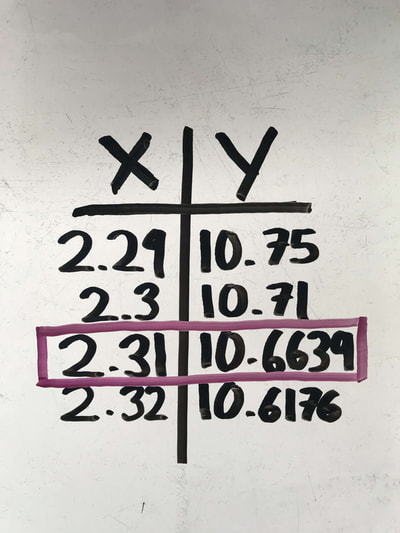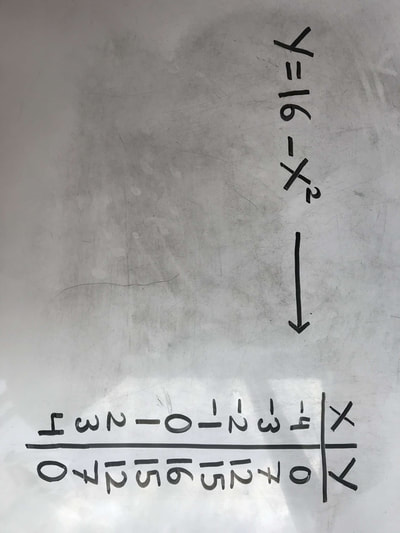Maximum rectangle
Problem statement: |
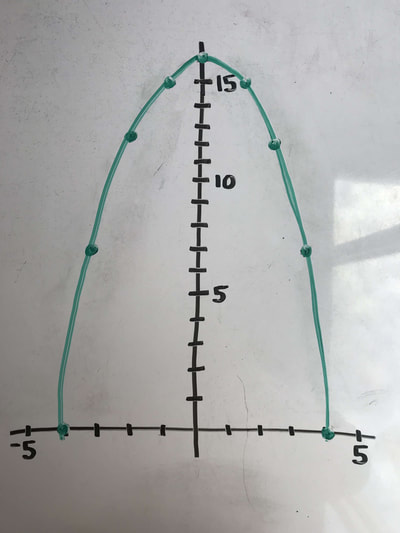
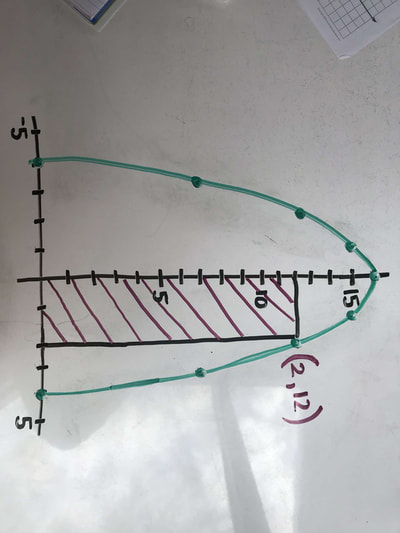
A rectangle has one corner on the graph of y= 16 -x^2, another at the origin, a third on the positive y-axis and the forth at the positive x-axis. If the area of the rectangle is a function of X, what is the value of X yields the largest area for the rectangle?
|
Process & solution: |
Initial Attempt:
My first idea of what this may look like was a really skinny rectangle. My question that I had in mind was, what does y=16-x^2 look like? Once we figured that out by plugging in whole numbers into x (-5 through 5), I tried drawing multiple squares only on whole numbers thinking that that is the only possible answer. I was wrong since there are infinite amount of numbers going into the decimal points. How we really solved it: Like I said, I plugged in whole numbers into the equation for x to solve for y. We created a chart then graphed it. To find the area of the largest rectangle, we used the formula a=x(16-x^2) which means what you plug in for x in the parenthesis will be y and y is the length, so length times width, which is the x. We noticed that 2 for x was the number with the highest area. 1 was 9 less than 2 of x, and 3 was 3 less than 2 of x. So this meant that it has to be a little bit over 2. To be sure, we tired 1.9 as x, this resulted of the area of 23.54, less than 24. So now we were certain that it was over 2. We made another chart with x on one side that included number ranging from 1.9 to 2.4. Now the number with the largest area we calculated to the hundredths decimal place was 2.3, it dropped again at 2.4. To take it even further, we made yet ANOTHER chart with the x from 2.29 to 2.32. We came closer to the exact number of the largest rectangle with the maximum area possible. 2.31 was for x with the area of 24.634. I thought at this point if we were going to try again to get the exact number. Then I was reminded that there are infinite numbers within that decimal so it is irrational. we were not going to get to that point so we stopped at the hundredths place of the x. We did all of that just for the area! Now for the maximum perimeter of a rectangle... To calculate the perimeter, it is length times length times width times width. We can put that into a formula 2(w+L). To do this, we plugged in what we got for width and then for the length (x and y). We made a chart of the x and the perimeter. Out of 1-3, 1 had the largest perimeter. To be sure that It was, I then tried .9 and it increased. So I continued all the way to .4. We then noticed that it maxes at .5 then decreases again at .4. So the perimeter is 32.50 |
individual/group test:
Unfortunately, I was out of town when it was the week to prepare for the test and the day of the test. Since that happened, I had to take both tests days after it was scheduled for. Me and one other person took it so it was more of a partnership test instead of a group one. During the test I feel okay about it which is rare for me to say because math is my strongest subject. I didn't complete the whole test because I completely forgot about the perimeter! I am to blame because I know that I should have studied while I was away from school and that I could have gone to tutoring the day before the make-up test. With my partner, I did not feel confident. I felt like I was doing all the work and it was more of an individual test but we both got credit for my work. My partner did understand some and helped with calculations but if it wasn't for me guiding then we wouldn't of gotten anywhere. My individual quiz went smoother. I understood all of it and am pretty confident turning it in. I personally work better alone than in a group because I plan out steps and I know that I will get it done, with group mates, sometimes they don't follow through. I never liked group quizzes but I know that it is to measure how we work in groups and putting our minds together to solve a difficult problem. I do not like how people in group quizzes can get an A on it for other peoples work. Yet, it does show on individual quizzes because the ones in the group that understand the math concepts get the higher grade.
Reflection:
This unit was fine for me learning it. Wasn't difficult nor easy. I did not preform as well as I wish I did on the group quiz though. For that, I would give myself an A- because I could have easily went to tutoring to understand the unit better. I don't know what I got the most out of, we weren't given packets to work on and with the group that I sit with right now, I don't feel like I'm being challenged and I am pushing my thinking. I feel like I am just helping them. But overall the problem was okay. For my style learning, I enjoy the lectures way more and I benefit more than big problems as well.