PROBLEM STATEMENT
First, King Arthur put numbers on the chairs beginning with 1 and continuing around the table, with one chair for each knight. He had the knights sit down so that every chair was occupied. King Arthur himself remained standing. Then King Arthur stood behind the knight in chair 1 and said, “You’re In.” Next, he moved to the knight in chair 2 and said, "You're Out,” and that knight left his seat and went off to stand at the side of the room to watch the rest of the game. Next, he moved to the knight in chair 3 and said, “You’re In.” Then he said, "You’re Out” to the knight in chair 4, and that knight left his seat and went to the side of the room. The king continued around the table in this manner. When he came back around to the knight in chair 1, he said either “You’re In” or “You’re Out,” depending on what he had said to the previous knight. (If the previous knight was “In,” then the knight in chair 1 was now “Out,” and vice versa.)
The king kept moving around and around the table alternately saying, "You're In" or "You're Out" to the knights who remained at the table. (If a chair was now empty, he simply skipped it.) He continued until only one knight was left sitting at the table. That knight was the winner. Of course, the number of knights varied from day to day, depending on who was sick, who was chasing dragons, and so on. Sometimes there were only a handful, and sometimes there were over a hundred!
In short, our job was to come up with a general rule or formula that quickly solves which chair would win depending on any number of knights!
The king kept moving around and around the table alternately saying, "You're In" or "You're Out" to the knights who remained at the table. (If a chair was now empty, he simply skipped it.) He continued until only one knight was left sitting at the table. That knight was the winner. Of course, the number of knights varied from day to day, depending on who was sick, who was chasing dragons, and so on. Sometimes there were only a handful, and sometimes there were over a hundred!
In short, our job was to come up with a general rule or formula that quickly solves which chair would win depending on any number of knights!
process

Individually:
When I first had a moment or two to think to myself and come up with questions to pose to my group, I went ahead and tested a few simple numbers out to see if there's some sort of pattern my eyes can catch right away. One was pretty self explanatory... King Arthur always started with the number one and that chair was in, all of the following even numbered chairs would be out, therefore an even number would never win. Another pattern I immediately saw was how the output depending how many seats there were restarted at different points. It restarted at 1, 2, 4, 8, 16... I noticed that if you multiply those numbers by 2 you get the number that follows on where it restarts again. That could be written as 2^0, 2^1, 2^2, 2^3, and so on. I knew that this was key information and that I had to share it with my group.
Group:
After taking and sharing my findings with my group, a lightbulb popped inside of my head. I know that those numbers on where it restarts is important and 1 is the base number on which we add on top off, so I decided to test an idea and it worked! If I take any number and subtracted the number bellow on which it restarted from, I then get that number and multiplied it by two because 3 would be too much (yes, I didn't have logic behind that choice), then I always got an even number so I then decided to add 1 because that's where it restarted and also because an even number plus 1 would turn odd. This idea worked for every number! The down side to that was I needed to figure out what was the number on where it restarted and that could take a long time if it is a bigger number.
When I first had a moment or two to think to myself and come up with questions to pose to my group, I went ahead and tested a few simple numbers out to see if there's some sort of pattern my eyes can catch right away. One was pretty self explanatory... King Arthur always started with the number one and that chair was in, all of the following even numbered chairs would be out, therefore an even number would never win. Another pattern I immediately saw was how the output depending how many seats there were restarted at different points. It restarted at 1, 2, 4, 8, 16... I noticed that if you multiply those numbers by 2 you get the number that follows on where it restarts again. That could be written as 2^0, 2^1, 2^2, 2^3, and so on. I knew that this was key information and that I had to share it with my group.
Group:
After taking and sharing my findings with my group, a lightbulb popped inside of my head. I know that those numbers on where it restarts is important and 1 is the base number on which we add on top off, so I decided to test an idea and it worked! If I take any number and subtracted the number bellow on which it restarted from, I then get that number and multiplied it by two because 3 would be too much (yes, I didn't have logic behind that choice), then I always got an even number so I then decided to add 1 because that's where it restarted and also because an even number plus 1 would turn odd. This idea worked for every number! The down side to that was I needed to figure out what was the number on where it restarted and that could take a long time if it is a bigger number.
solution
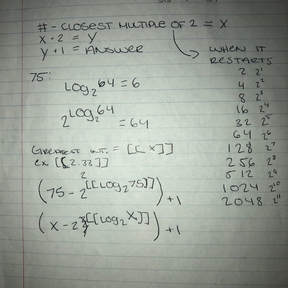
To put my findings in a formula, Mr. B helped me by using something that we learned as a class not too long ago. Logarithms! Written out it looked sort of funky.
W= Winner
K= Knights
S= Solution
S=(K-2^[[Log2K]])+1
An example of that could be a tiny number like 25 in which I could solve using the way I thought out step by step, or a larger number such as 15,873 in which I could find the number where it restarts but the formula is much more effective.
25-16= 9, 9 times 2= 18, 18 + 1= 19
S=(5,000-2^[[Log2(5,000)]])+1
S=(5,000-2^[[12.287]])+ 1
S=(5,000-2^12)+ 1
S=(904)+ 1
S= 905
W= Winner
K= Knights
S= Solution
S=(K-2^[[Log2K]])+1
An example of that could be a tiny number like 25 in which I could solve using the way I thought out step by step, or a larger number such as 15,873 in which I could find the number where it restarts but the formula is much more effective.
25-16= 9, 9 times 2= 18, 18 + 1= 19
S=(5,000-2^[[Log2(5,000)]])+1
S=(5,000-2^[[12.287]])+ 1
S=(5,000-2^12)+ 1
S=(904)+ 1
S= 905
Evaluation/reflection
What defiantly pushed my thinking was how to put my findings all into one formula. I honestly would have kept it as is and just say that there are 3 steps to the answer. I understood logarithms and also the new term about the greatest integer wasn't so hard. Without the help from Mr. B, I don't think that I would be able to make the formula. I do recall when I needed help with figuring that part out but I feel that whenever I get stuck that I try a couple different things then I ask my group, but when I still don't understand I then go to the teacher. I feel like individually I did great, but I do notice that I enjoy working on my own for most of the time. This is because I know my own work style and I can get things done on time, and I also like to move at a very quick pace once I understand a topic. During the group quiz, I am positive that I preformed very well. I already knew the steps to take and recognized what the formula may look like. What stumped me was how the formula I came up with did not work for the numbers in which the winner restarts on. I then made a new formula and it worked but I couldn't combined. I'm sure that if I had a few hints if it wasn't a group quiz, I would have been able to do so.
